定长滑动窗口
1456. 定长子串中元音的最大数目
给你字符串 s 和整数 k 。
请返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数。
英文中的 元音字母 为(a, e, i, o, u)。
示例 1:
输入:s = “abciiidef”, k = 3
输出:3
解释:子字符串 “iii” 包含 3 个元音字母。
示例 2:
输入:s = “aeiou”, k = 2
输出:2
解释:任意长度为 2 的子字符串都包含 2 个元音字母。
示例 3:
输入:s = “leetcode”, k = 3
输出:2
解释:”lee”、”eet” 和 “ode” 都包含 2 个元音字母
思路
对于下图的字符串 abci,假如我们已经计算出了子串 abc 的元音个数,那么从子串 abc 到子串 bci,只需要考虑移除(离开窗口)的字母 a 是不是元音,以及添加(进入窗口)的字母 i 是不是元音即可,因为中间的字母 b 和 c 都在这两个子串中。
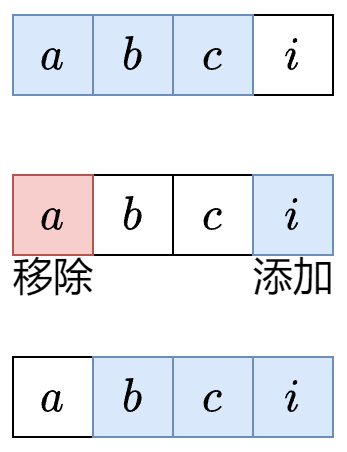
示例 1,s=abciiidef, k=3。
从左到右遍历 s。
首先统计前 k−1=2 个字母的元音个数,这有 1 个。
s[2]=c 进入窗口,此时找到了第一个长为 k 的子串 abc,现在元音个数有 1 个,更新答案最大值。然后 s[0]=a 离开窗口,现在元音个数有 0 个。
s[3]=i 进入窗口,此时找到了第二个长为 k 的子串 bci,现在元音个数有 1 个,更新答案最大值。然后 s[1]=b 离开窗口,现在元音个数有 1 个。
s[4]=i 进入窗口,此时找到了第三个长为 k 的子串 cii,现在元音个数有 2 个,更新答案最大值。然后 s[2]=c 离开窗口,现在元音个数有 2 个。
s[5]=i 进入窗口,此时找到了第四个长为 k 的子串 iii,现在元音个数有 3 个,更新答案最大值。然后 s[3]=i 离开窗口,现在元音个数有 2 个。
s[6]=d 进入窗口,此时找到了第五个长为 k 的子串 iid,现在元音个数有 2 个,更新答案最大值。然后 s[4]=i 离开窗口,现在元音个数有 1 个。
s[7]=e 进入窗口,此时找到了第六个长为 k 的子串 ide,现在元音个数有 2 个,更新答案最大值。然后 s[5]=i 离开窗口,现在元音个数有 1 个。
s[8]=f 进入窗口,此时找到了第七个长为 k 的子串 def,现在元音个数有 1 个,更新答案最大值。遍历结束。
因此,可以不断循环递增窗口右端点i,并判断新增的端点是否为元音字母,如果是则答案加1
之后判断现在是否形成窗口,窗口左端点下标为i-k+1(k为窗口长度),若i-k+1<0则continue,>0则用max记录新答案
之后窗口整体右移一位,因此要判断窗口左端点是否为元音字母,若是则答案减1
class Solution {
public int maxVowels(String s, int k) {
int len = s.length();
int preans = 0 , ans = 0;
//枚举窗口右端点
for(int i=0;i<len;i++){
//1.右端点进入窗口
char ch = s.charAt(i);
if(ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u'){
preans++;
}
//窗口左端点小于0,说明尚未形成第一个窗口
if(i-k+1<0)continue;
//答案已经等于理论最大值,无需再循环
if(preans == k)return k;
//2.更新答案
ans = Math.max(preans,ans);
//3.左端点离开窗口,为下一个循环做准备
char chl = s.charAt(i-k+1);
if(chl == 'a' || chl == 'e' || chl == 'i' || chl == 'o' || chl == 'u'){
preans--;
}
}
return ans;
}
}注:也可以先把s变为字符数组 char[] arr = s.toCharArray();,这样就不用charAt了
643. 子数组最大平均数 I
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
示例 1:
输入:nums = [1,12,-5,-6,50,3], k = 4
输出:12.75
解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
示例 2:
输入:nums = [5], k = 1
输出:5.00000
提示:
- n == nums.length
- 1 <= k <= n <= 1e5
- -1e4 <= nums[i] <= 1e4
class Solution {
public double findMaxAverage(int[] nums, int k) {
double sum = 0 , ans = -1e9;//因为数组中可能会有负数
for(int i=0;i<nums.length;i++){
sum += nums[i];
if(i-k+1<0)continue;
ans = Math.max(ans,sum/k);
sum -= nums[i-k+1];
}
return ans;
}
}2090. 半径为 k 的子数组平均值
给你一个下标从 0 开始的数组 nums ,数组中有 n 个整数,另给你一个整数 k 。
半径为 k 的子数组平均值 是指:nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值,即下标在 i - k 和 i + k 范围(含 i - k 和 i + k)内所有元素的平均值。如果在下标 i 前或后不足 k 个元素,那么 半径为 k 的子数组平均值 是 -1 。
构建并返回一个长度为 n 的数组 avgs ,其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。
x 个元素的 平均值 是 x 个元素相加之和除以 x ,此时使用截断式 整数除法 ,即需要去掉结果的小数部分。
例如,四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75,截断后得到 2 。
示例 1:

输入:nums = [7,4,3,9,1,8,5,2,6], k = 3
输出:[-1,-1,-1,5,4,4,-1,-1,-1]
解释:
- avg[0]、avg[1] 和 avg[2] 是 -1 ,因为在这几个下标前的元素数量都不足 k 个。
- 中心为下标 3 且半径为 3 的子数组的元素总和是:7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
使用截断式 整数除法,avg[3] = 37 / 7 = 5 。 - 中心为下标 4 的子数组,avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心为下标 5 的子数组,avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ,因为在这几个下标后的元素数量都不足 k 个。
示例 2:
输入:nums = [100000], k = 0
输出:[100000]
解释:
- 中心为下标 0 且半径 0 的子数组的元素总和是:100000 。
avg[0] = 100000 / 1 = 100000 。
示例 3:
输入:nums = [8], k = 100000
输出:[-1]
解释:
- avg[0] 是 -1 ,因为在下标 0 前后的元素数量均不足 k 。
提示:
n == nums.length
1 <= n <= 1e5
0 <= nums[i], k <= 1e5
注:此题中窗口的总和可能超过int的最大值!要用long
class Solution {
public int[] getAverages(int[] nums, int k) {
int len = nums.length;
//滑动窗口长度
int size = 2 * k + 1;
int[] arr = new int[len];
Arrays.fill(arr,-1);//初始化全为-1
long sum = 0; //窗口元素总和(注意类型!)
for(int i=0;i<len;i++){
sum += nums[i];
//不足k个元素(左边)
if(i-k<0)continue;
//不足k个元素(右边),直接通过第7行的fill!
//size为滑动窗口的长度
if(i-size+1<0)continue;
//窗口中心记录答案
arr[i-k] = (int)(sum/size);
sum -= nums[i-k*2];
}
return arr;
}
}- 来源:力扣
- 作者:灵茶山艾府

